Engineering rollers

In Versions 1 and 2, the roller always pivots on a vertex, even at the top and bottom, and the distance to the opposite contact point is always the same.

In Version 3, the width of the non-round roller at any point is defined by a straight line that runs through one of the vertices of the triangle and through the triangle itself. Each such straight line is the sum of two radii—the radius of one large arc and the radius of one small arc. For example, the straight line PO in the diagram below (click to enlarge) is the sum of the radii of arc HG (a large arc) and arc DE (a small arc).

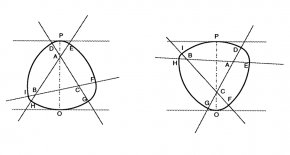
Suppose you have a roller like the one shown in the diagram above. Let’s say the roller is resting on point O. As the roller rolls on arc HG, with its resting point approaching H, the board on top of the roller will be rolling on arc DE. The board will remain level because the roller’s width (which is the sum of the radius of arc DE and the radius of arc HG) will be constant.

Suppose the roller rolls until it rests on point H. Its width is still the sum of two radii—the radius of arc HI and the radius of arc EF. Because arc HI and arc HG have point H in common, and because arc DE and arc EF have point E in common, the width of the roller must still be constant. As the roller continues rolling and reaches point I, the same argument applies, and the width of the roller is always the same.

When you tried to choose a center for your non-round roller, you might logically have chosen the triangle’s centroid. Another logical choice would be the point halfway between the top and bottom of the roller for a particular orientation. Neither of these points, however, stays at a constant height as the roller rolls. Instead, they describe an up-and-down motion. As you observed, no point on the roller stays a constant height as the roller rolls. For this reason, the rollers would make lousy car wheels. (Where would you put the axle?)